hukum Hardy-Weinberg , juga disebut top atau Hardy-Weinberg, adalah teorema matematika yang menggambarkan populasi hipotetis diploid reproduksi seksual yang tidak berkembang – frekuensi alel tidak berubah dari generasi ke generasi.
Prinsip ini mengasumsikan lima kondisi yang diperlukan agar populasi tetap konstan: tidak adanya aliran gen, tidak adanya mutasi, perkawinan acak, tidak adanya seleksi alam, dan ukuran populasi yang sangat besar. Dengan cara ini, tanpa adanya kekuatan-kekuatan ini, populasi tetap dalam keseimbangan.
Sumber: Barbirossa [GFDL (http://www.gnu.org/copyleft/fdl.html) atau CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/)], melalui Wikimedia Commons
Ketika salah satu asumsi di atas tidak terpenuhi, perubahan terjadi. Untuk alasan ini, seleksi alam, mutasi, migrasi, dan pergeseran genetik adalah empat mekanisme evolusioner.
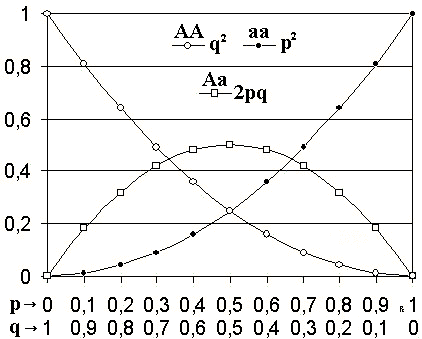
Menurut caral ini, ketika frekuensi alel suatu populasi adalah p dan q, frekuensi genotipe akan menjadi p 2 , 2 pq dan q 2 .
Kita dapat menerapkan keseimbangan Hardy-Weinberg dalam menghitung frekuensi alel tertentu yang menarik, misalnya, untuk memperkirakan proporsi heterozigot dalam populasi manusia. Kita juga dapat memverifikasi apakah suatu populasi berada dalam keseimbangan dan mengajukan hipotesis bahwa gaya bekerja pada populasi tersebut.
Indeks artikel
Perspektif sejarah
Prinsip Hardy-Weinberg lahir pada tahun 1908 dan mendapatkan namanya dari ilmuwannya GH Hardy dan W. Weinberg, yang secara independen mencapai kesimpulan yang sama.
Sebelum itu, ahli biologi lain bernama Udny Yule telah menangani masalah ini pada tahun 1902. Yule memulai dengan satu set gen di mana frekuensi kedua alel adalah 0,5 dan 0,5. Ahli biologi menunjukkan bahwa frekuensi dipertahankan selama generasi berikutnya.
Meskipun Yule menyimpulkan bahwa frekuensi alelik dapat dijaga tetap stabil, interpretasinya terlalu literal. Dia percaya bahwa satu-satunya keadaan keseimbangan ditemukan ketika frekuensi sesuai dengan nilai 0,5.
Yule dengan hangat mendiskusikan temuan barunya dengan RC Punnett – yang dikenal luas dalam genetika karena menemukan “alun-alun Punnett” yang terkenal. Meskipun Punnett tahu bahwa Yule salah, dia tidak dapat menemukan cara matematis untuk membuktikannya.
Untuk alasan ini, Punnett menghubungi teman matematikawannya, Hardy, yang berhasil menyelesaikannya dengan segera, mengulangi perhitungan menggunakan variabel umum, dan bukan nilai tetap 0,5 seperti yang dilakukan Yule.
Genetika populasi
Genetika populasi tujuan untuk mempelajari kekuatan yang mengarah pada perubahan alel frekuensi pada populasi, mengintegrasikan teori Charles Darwin tentang evolusi melalui seleksi alam dan genetika Mendel. Saat ini, prinsip-prinsipnya memberikan dasar teoretis untuk memahami banyak aspek biologi evolusioner.
Salah satu ide penting dari genetika populasi adalah hubungan antara perubahan kelimpahan relatif sifat dan perubahan kelimpahan relatif alel yang mengaturnya, dijelaskan oleh prinsip Hardy-Weinberg. Faktanya, teorema ini memberikan kerangka konseptual untuk genetika populasi.
Ditinjau dari genetika populasi, konsep evolusi adalah sebagai berikut: perubahan frekuensi alel dari generasi ke generasi. Ketika tidak ada perubahan, tidak ada evolusi.
Apa yang dimaksud dengan keseimbangan Hardy-Weinberg?
Kesetimbangan Hardy-Weinberg adalah caral nol yang memungkinkan kita untuk menentukan perilaku gen dan frekuensi alel lintas generasi. Dengan kata lain, itu adalah caral yang menggambarkan perilaku gen dalam populasi, di bawah serangkaian kondisi tertentu.
Notasi
Dalam teorema Hardy-Weinbergm frekuensi alel A (alel dominan) dilambangkan dengan huruf p, sedangkan frekuensi alel a (alel resesif) dilambangkan dengan huruf q.
Frekuensi genotipe yang diharapkan adalah p 2 , 2 pq dan q 2 , untuk homozigot dominan ( AA ), heterozigot ( Aa ) dan homozigot resesif ( aa ), masing-masing.
Jika hanya ada dua alel pada lokus tersebut, jumlah frekuensi kedua alel tersebut harus sama dengan 1 ( p + q = 1). Ekspansi binomial ( p + q ) 2 mewakili frekuensi genotipe p 2 + 2 pq + q 2 = 1.
Contoh
Dalam suatu populasi, individu-individu yang membentuknya kawin silang untuk menghasilkan keturunan. Secara umum, kita dapat menunjukkan aspek terpenting dari siklus reproduksi ini: produksi gamet, peleburannya untuk menghasilkan zigot, dan perkembangan embrio untuk menghasilkan generasi baru.
Bayangkan bahwa kita dapat melacak proses gen Mendel dalam peristiwa yang disebutkan. Kita melakukan ini karena kita ingin mengetahui apakah dan mengapa suatu alel atau genotipe akan bertambah atau berkurang frekuensinya.
Untuk memahami bagaimana gen dan frekuensi alel bervariasi dalam suatu populasi, kita akan mengikuti produksi gamet dari sekumpulan tikus. Dalam contoh hipotetis kita, perkawinan terjadi secara acak, di mana semua sperma dan telur dicampur secara acak.
Dalam kasus tikus, asumsi ini tidak benar dan hanya penyederhanaan untuk memudahkan perhitungan. Namun, pada beberapa kelompok hewan, seperti echinodermata tertentu dan organisme air lainnya, gamet dikeluarkan dan bertabrakan secara acak.
Tikus generasi pertama
Sekarang, mari kita fokuskan perhatian kita pada lokus tertentu, dengan dua alel: A dan a . Mengikuti hukum yang diucapkan oleh Gregor Mendel , setiap gamet menerima alel dari lokus A. Misalkan 60% ovula dan sperma menerima alel A , sedangkan 40% sisanya menerima alel a .
Jadi, frekuensi alel A adalah 0,6 dan frekuensi alel a adalah 0,4. Kelompok gamet ini akan ditemukan secara acak untuk menghasilkan zigot.Berapa peluang mereka akan membentuk masing-masing dari tiga kemungkinan genotipe? Untuk melakukan ini, kita harus mengalikan probabilitas sebagai berikut:
Genotipe AA : 0,6 x 0,6 = 0,36.
Genotipe Aa : 0,6 x 0,4 = 0,24. Dalam kasus heterozigot, ada dua bentuk asalnya. Yang pertama sperma membawa alel A dan ovum membawa alel a , atau sebaliknya, sperma membawa ovum a dan A . Oleh karena itu kita tambahkan 0.24 + 0.24 = 0.48.
Genotipe aa : 0,4 x 0,4 = 0,16.
Tikus generasi kedua
Sekarang, bayangkan zigot ini berkembang dan menjadi tikus dewasa yang akan kembali menghasilkan gamet, apakah kita mengharapkan frekuensi alel sama atau berbeda dari generasi sebelumnya?
Genotipe AA akan menghasilkan 36% gamet, sedangkan heterozigot akan menghasilkan 48% gamet, dan genotipe aa 16%.
Untuk menghitung frekuensi alel baru, kita menambahkan frekuensi homozigot ditambah setengah dari heterozigot, sebagai berikut:
Frekuensi alel A : 0,36 + (0,48) = 0,6.
Frekuensi alel a : 0,16 + (0,48) = 0,4.
Jika kita membandingkannya dengan frekuensi awal, kita akan menyadari bahwa keduanya identik. Oleh karena itu, menurut konsep evolusi, karena tidak ada perubahan frekuensi alel dari generasi ke generasi, populasi berada dalam keseimbangan – tidak berevolusi.
Asumsi Kesetimbangan Hardy-Weinberg
Kondisi apa yang harus dipenuhi populasi sebelumnya agar frekuensi alelnya tetap konstan selama beberapa generasi? Dalam caral keseimbangan Hardy-Weinberg, populasi yang tidak berevolusi memenuhi asumsi berikut:
Populasinya sangat besar
Populasi harus berukuran sangat besar untuk menghindari efek stokastik atau acak dari pergeseran gen.
Ketika populasi kecil, efek pergeseran gen (perubahan acak dalam frekuensi alel, dari satu generasi ke generasi lain) karena kesalahan pengambilan sampel jauh lebih besar dan dapat menyebabkan fiksasi atau hilangnya alel tertentu.
Tidak ada aliran gen
Migrasi tidak ada dalam populasi, sehingga alel yang dapat mengubah frekuensi gen tidak dapat tiba atau pergi.
Tidak ada mutasi
Mutasi adalah perubahan dalam urutan DNA , dan mereka dapat memiliki penyebab yang berbeda. Perubahan acak ini memodifikasi kumpulan gen dalam populasi, dengan pengenalan atau eliminasi gen dalam kromosom.
Perkawinan acak
Pencampuran gamet harus dilakukan secara acak – seperti asumsi yang kita gunakan pada contoh tikus. Oleh karena itu, tidak boleh ada pilihan kawin di antara individu-individu dalam populasi, termasuk perkawinan sedarah (reproduksi individu yang berkerabat).
Ketika perkawinan tidak acak, tidak menyebabkan perubahan frekuensi alel dari satu generasi ke generasi berikutnya, tetapi dapat menghasilkan penyimpangan dari frekuensi genotipe yang diharapkan.
Tidak ada pilihan
Tidak ada perbedaan keberhasilan reproduksi individu dengan genotipe berbeda yang dapat mengubah frekuensi alel dalam populasi.
Dengan kata lain, dalam populasi hipotetis semua genotipe memiliki probabilitas yang sama untuk bereproduksi dan bertahan hidup.
Ketika suatu populasi tidak memenuhi lima kondisi ini, hasilnya adalah evolusi. Logikanya, populasi alami tidak memenuhi asumsi ini. Oleh karena itu, caral Hardy-Weinberg digunakan sebagai hipotesis nol yang memungkinkan kita membuat perkiraan perkiraan frekuensi gen dan alel.
Selain tidak adanya kelima kondisi tersebut, ada kemungkinan penyebab lain yang menyebabkan populasi tidak seimbang.
Salah satunya terjadi ketika lokus terkait dengan jenis kelamin atau fenomena distorsi dalam segregasi atau dorongan meiosis (ketika setiap salinan gen atau kromosom tidak ditransmisikan dengan kemungkinan yang sama ke generasi berikutnya).
Masalah terpecahkan
Frekuensi pembawa fenilketonuria
Di Amerika Serikat, diperkirakan satu dari 10.000 bayi baru lahir memiliki kondisi yang disebut fenilketonuria.
Gangguan ini hanya diekspresikan pada homozigot resesif pada gangguan metabolisme. Mengetahui data tersebut, berapa frekuensi pembawa penyakit dalam populasi?
Penyelesaian
Untuk menerapkan persamaan Hardy-Weinberg kita harus berasumsi bahwa pilihan pasangan tidak terkait dengan gen yang terkait dengan patologi dan tidak ada perkawinan sedarah.
Selanjutnya, kita berasumsi bahwa tidak ada fenomena migrasi di Amerika Serikat, tidak ada mutasi fenilketonuria baru, dan kemungkinan reproduksi dan kelangsungan hidup adalah sama antara genotipe.
Jika kondisi yang disebutkan di atas benar, kita dapat menggunakan persamaan Hardy-Weinberg untuk melakukan perhitungan yang relevan dengan masalah.
Kita tahu bahwa ada satu kasus penyakit setiap 10.000 kelahiran, jadi q 2 = 0,0001 dan frekuensi alel resesif akan menjadi akar kuadrat dari nilai ini: 0,01.
Karena p = 1 – q , kita mendapatkan bahwa p adalah 0,99. Sekarang kita memiliki frekuensi kedua alel: 0,01 dan 0,99. Frekuensi pembawa mengacu pada frekuensi heterozigot yang dihitung sebagai 2 pq . Jadi, 2 pq = 2 x 0,99 x 0,01 = 0,0198.
Ini setara dengan sekitar 2% dari populasi. Ingatlah bahwa ini hanya hasil perkiraan.
Apakah populasi berikut berada dalam kesetimbangan Hardy-Weinberg?
Jika kita mengetahui jumlah masing-masing genotipe dalam populasi, kita dapat menyimpulkan jika berada dalam kesetimbangan Hardy-Weinberg. Langkah-langkah untuk mengatasi jenis masalah tersebut adalah sebagai berikut:
- Hitung frekuensi genotipe yang diamati ( D, H dan R )
- Hitung frekuensi alel ( p dan q )
p = D + ½ H
q = R + ½ H
- Hitung frekuensi genotipe yang diharapkan ( p 2 , 2 pq dan q 2 )
- Hitung angka yang diharapkan ( p 2 , 2 pq dan q 2 ), kalikan nilai-nilai ini dengan jumlah total individu
- Kontras nomor yang diharapkan dengan yang diamati dengan Pearson X 2 tes .
Populasi kupu-kupu
Sebagai contoh, kita ingin memverifikasi apakah populasi kupu-kupu berikut berada dalam kesetimbangan Hardy-Weinberg: terdapat 79 individu dari genotipe dominan homozigot ( AA ), 138 individu heterozigot ( Aa ) dan 61 individu homozigot resesif ( aa ).
Langkah pertama adalah menghitung frekuensi yang diamati. Kita melakukan ini dengan membagi jumlah individu per genotipe dengan jumlah total individu:
D = 79/278 = 0,28
H = 138/278 = 0,50
R = 61/278 = 0,22
Untuk memverifikasi apakah saya telah melakukannya dengan baik, ini adalah langkah pertama, saya menambahkan semua frekuensi dan harus memberikan 1.
Langkah kedua adalah menghitung frekuensi alel.
p = 0,28 + (0,50) = 0,53
q = 0,22 + (0,50) = 0,47
Dengan data ini, saya dapat menghitung frekuensi genotipe yang diharapkan ( p 2 , 2 pq dan q 2 )
p 2 = 0,28
2 pq = 0,50
q 2 = 0,22
Saya menghitung angka yang diharapkan, mengalikan frekuensi yang diharapkan dengan jumlah individu. Dalam hal ini, jumlah individu yang diamati dan diharapkan adalah identik, sehingga saya dapat menyimpulkan bahwa populasi berada dalam keseimbangan.
Bila angka yang diperoleh tidak identik, saya harus menerapkan uji statistik tersebut ( Pearson’s X 2 ).
Referensi
- Andrews, C. (2010). Prinsip Hardy-Weinberg. Pengetahuan Pendidikan Alam 3 (10): 65.
- Audesirk, T., Audesirk, G., & Byers, BE (2004). Biologi: ilmu pengetahuan dan alam . Pendidikan Pearson.
- Freeman, S., & Herron, JC (2002). Analisis evolusioner . Aula Prentice.
- Futuyma, DJ (2005). Evolusi. Sinauer.
- Hickman, CP, Roberts, LS, Larson, A., Ober, WC, & Garrison, C. (2001). Prinsip-prinsip zoologi yang terintegrasi (Vol. 15). New York: McGraw-Hill.
- Soler, M. (2002). Evolusi: dasar Biologi . Proyek Selatan.

